Примеры годографов Найквиста астатических САР и САР с чисто мнимыми корнями

Устойчивая САР с астатизмом первого порядка.

Устойчивая САР с астатизмом второго порядка.

Устойчивая САР с астатизмом третьего порядка.

Неустойчивая САР с консервативным звеном.

Устойчивая САР с консервативным звеном (коррекция выполнена фазовращающим звеном).

САР на колебательной границе устойчивости.

Абсолютно устойчивая САР (устойчива при любом уменьшении K).

Неустойчивая САР.

Условно устойчивая САР (только при изменении K в некотором диапазоне).

Принцип 1 (для шин)

Все элементы и узлы ненаправленного графа соединяются шинами, в которых есть два проводника распространяющие сигналы в противоположных направлениях. (Упомянутые сигналы – это физические величины первого и второго рода конкретного энергетического домена, для которых формулируются постулаты о сохранении материи и энергетического потенциала).

Принцип 2 (для элементов)

Все элементы графа должны быть двухвыводными. (Схема замещения любого устройства с большим количеством выводов должна состоять из фундаментальных двухвыводных элементов и узлов). Оба вывода у элементов должны быть оборудованы разъемами для подключения двухпроводных шин.

Принцип 3 (для узлов)

Узлы бывают двух типов: распределяющие и аккумулирующие. Узлы ненаправленного графа трехвыводные. (Узлы, в которых сходится большее количество ветвей, строятся каскадированием трехвыводных узлов). Каждый вывод узла должен иметь разъем для подключения двухпроводных шин.

Принцип 4 (для разъемов)

Элементы графа и его шины оборудуются разъемами "мама" и "папа". Половина узлов ненаправленного графа оборудуется одним разъемом "папа" и двумя разъемами "мама". Вторая половина узлов оборудуется одним разъемом "мама" и двумя разъемами "папа". (Графический интерфейс моделирующих программ не должен отображать этой особенности ненаправленного графа. Программы самостоятельно выбирают тип узлов, "скрыто переворачивают" элементы графа и шины для правильной коммутации).

Принцип поточного исполнения блок-схем (моделей)

Программы математического моделирования динамических систем относятся к графическим средам разработки иерархически структурированных программ верхнего уровня, и часть из них основана на поточной модели управления. Поточная модель управления – это основополагающее понятие для таких програм, как VisSim, MBTY, Simulink, Easy5. Приведем определение:

Поточная модель управления (Data Flow)

Модель программирования, в которой инструкции, процедуры или функции выполняются только тогда, когда все входные данные (т.е. параметры и аргументы) готовы. Альтернативной моделью программирования является командное управление (Control Flow) в которой счетчик команд контролирует переход в памяти программ от одной команды к другой при их последовательном выполнении.

Рассмотрим пример:

Система уравнений модели составленная пользователем	Упорядоченный программой информационный поток
a) w = log(r) b) e = 1 c) r = e - q d) q = sin(e)	1) e = 1 2) q = sin(e) 3) r = e - q 4) w = log(r)

Для написания программ (создания моделей) используются графические языки, с помощью которых выполняется описание процессов преобразования данных в форме функциональных схем, блок-схем, схем физических принципиальных, мнемосхем, и прочее. Представим блок-схему для рассмотренного в примере информационного потока.

Статический информационный поток, составленный с помощью элементарных библиотечных блоков программы VisSim

Анализируя рисунок, легко заметить, что в любом информационном потоке данные распространяются от источников сигнала к приемникам. Очевидно, что в одном потоке могут существовать ветви, параллельные каналы и обратные связи. Могут существовать зависимые и независимые параллельные потоки. В случае если с течением времени источники сигнала меняют свое значение, то появляется смысл в повторном расчете потока. Такой информационный поток называется динамическим, а каждый повторный расчет называется шагом симуляции. Наиболее развитые языки графического программирования (G-язык среды программирования LabVIEW) кроме формирования информационных потоков позволяют программировать их исполнение, а в случае определения независимых параллельных потоков (мультизадачности) обеспечивают требуемый вид синхронизации.

Принцип управления по отклонению

Достоинства:

ООС приводит к уменьшению ошибки не зависимо от факторов ее вызвавших (изменений параметров регулируемого объекта или внешних условий).

Недостатки:

В системах с ОС возникает проблема устойчивости.

В системах принципиально невозможно добиться абсолютной инвариантности к возмущениям. Стремление добиться частичной инвариантности (не 1-ыми ОС) приводит к усложнению системы и ухудшению устойчивости.

Принцип управления по внешнему возмущению

Достоинства:

Можно добиться полной инвариантности к определенным возмущениям.

Не возникает проблема устойчивости системы, т.к. нет ОС.

Недостатки:

Большое количество возмущений требует соответствующего количества компенсационных каналов.

Изменения параметров регулируемого объекта приводят к появлению ошибок в управлении.

Можно применять только к тем объектам, чьи характеристики четко известны.

Принципы автоматического регулирования

По принципу управления САУ можно разбить на три группы:

С регулированием по внешнему воздействию - принцип Понселе (применяется в незамкнутых САУ).

С регулированием по отклонению - принцип Ползунова-Уатта (применяется в замкнутых САУ).

С комбинированным регулированием. В этом случае САУ содержит замкнутый и разомкнутый контуры регулирования.

Приведенные весовая и передаточная функции разомкнутой импульсной системы

Если ИИЭ выдает решетчатую функцию, то можно ввести понятие "приведенной весовой функции" - wп. Это отношение выходного сигнала

y(t) к значению единственной дискреты xo поданной на вход экстраполятора.

Если ИИЭ выдает последовательность типа d-функций, то для непрерывной части совместно с экстраполятором можно вывести понятие приведенной непрерывной передаточной функции:

Wп(s)= Wэ(s) Wo(s), при этом Wп(s) = L{ wп(t) }.

Проблематика, задачи и цели моделирования

В теории моделирования основными являются проблемы: разработки универсальных подходов к построению моделей, точности симуляции движения их координат, оценки величин погрешностей, адекватности получаемых результатов, идентификации изучаемых систем, синтеза технических устройств и гипотез.

Задачи общей теории моделирования заключаются в решении перечисленных проблем. При поиске решений используются:

Методы теории подобия

Методы теории расчета цепей

Методы теории систем автоматического управления

Численные методы

Глобальными целями моделирования являются вопросы изучения природы систем, возможностей их структурного развития и прогнозирование поведения.

Процессы протекающие в системах ЦУ

Рабочие файлы: [Субгармонические автоколебания]

Дискретная природа ЦВМ определила наличие 2-х процессов в системах ЦУ: 1) дискретизации сигналов по времени (получение решетчатой функции), и 2) квантования сигналов по уровню (АЦ и ЦА преобразования).

Дискретизация сигналов по времени делает систему дискретной, а квантование по уровню - нелинейной. Оба процесса сопровождаются возникновением методических погрешностей.

Выбор частоты дискретизации производится исходя из ширены полосы пропускания или из времени регулирования замкнутой системы. Разумные частоты дискретизации в 6..10 раз больше ширены полосы пропускания или от 2-х до 4-х дискретных отсчетов за время нарастания, в противном случае качество системы будет резко ухудшаться.

Количество ступеней квантования по уровню оказывает существенное влияние на динамические свойства систем. При недостаточном их количестве могут возникать периодические режимы переключений между дискретами (автоколебания).

Может случиться так, что выполняемые ЦВМ задачи (опрос датчиков, расчет программы, формирование информационных потоков, запись в порты вывода) могут быть выполнены только при систематической задержке синтезируемого воздействия на один такт дискретизации. В таком случае в системе с ЦВМ появится запаздывание t, которое должно быть учтено оператором запаздывания z -1 и, возможно, смещенной ПФ

W(z, e).

Обычно количество ступеней квантования по уровню велико, поэтому его влиянием пренебрегают. Это делает систему, линейной и позволяет использовать математический аппарат импульсных систем.

Проектирование цифровых фильтров второго порядка с бесконечной импульсной характеристикой

Рабочие файлы: [Аналоговые прототипы дискретных фильтров]

Примеры ЧХ дискретного фильтра: [z2_tf_fr.vsm][z2_tf_fr.mcd]

Передаточную функцию (ПФ) для дискретного фильтра любого типа можно получить из ПФ аналогового прототипа посредствам Билинейного преобразования (БЛП). Одновременно БЛП может быть использовано для масштабирующих операций в частотном домене. В частности для смещения полосы пропускания и регулировки ее ширины.

Дискретная ПФ фильтра второго порядка имеет вид:

(1)

b0 + b1*z^-1 + b2*z^-2 H(z) = ------------------------ a0 + a1*z^-1 + a2*z^-2

Для сокращения нагрузки на ЦВМ шесть коэффициентов z-ПФ могут быть заменены эквивалентными, один из которых будет равен единице (одна из шести операций умножения будет сокращена). Если проектируемая z-ПФ лишь одна из нескольких включенных последовательно, то можно привести к единице еще один коэффициент, за счет коррекции общего коэффициента передачи цепочки фильтров или системы. Тогда z-ПФ будет иметь вид:

(2)

(b0/a0) + (b1/a0)*z^-1 + (b2/a0)*z^-2 H(z) = --------------------------------------- 1 + (a1/a0)*z^-1 + (a2/a0)*z^-2

или

(3)

1 + (b1/b0)*z^-1 + (b2/b0)*z^-2 H(z) = (b0/a0) * --------------------------------- 1 + (a1/a0)*z^-1 + (a2/a0)*z^-2

Дальнейшее сокращение операций умножения возможно, если z-ПФ имеет пары равных коэффициентов.

Рекуррентный алгоритм, реализующий z-ПФ (2), должен рассчитывать следующее разностное уравнение (РУ):

(4)

y[n] = (b0/a0)*x[n] + (b1/a0)*x[n-1] + (b2/a0)*x[n-2] - (a1/a0)*y[n-1] - (a2/a0)*y[n-2]

Программы и законы регулирования

Рабочие файлы: [Нелинейные законы]

Программа регулирования

План формирования задающего воздействия g(t) на систему.

Программа регулирования может быть:

временной: y = y(t);

параметрической:   y = y(s1, s2, s3, ..., sn).

Например, временная программа приготовления пищи (лапшу варить 12 мин.), или параметрическая программа посадки самолета на палубу авианосца (в зависимости от: бокового ветра, изменений координат посадочной полосы, массы остатка топлива, ...).

Закон регулирования

Зависимость, по которой формируется регулирующее воздействие u(t)

на объект из первичной информации: g(t) и/или x(t) и, возможно, f (t).

Законы регулирования бывают:

линейные:

нелинейные:   F1(u, du/dt, ...) = F2(x, dx/dt, ...; g, ...; f, ...) .

Классификация нелинейных законов регулирования:

Функциональные.

Логические.

Параметрические.

Оптимизирующие.

Примеры статических функциональных нелинейностей в законах:

Примеры динамических функциональных нелинейностей в законах:

Пример логического нелинейного закона:

Если |x| < 0.2Gm, тогда u = k1 x ; Если |x| > 0.2Gm, тогда u = k2 x ; где: k1 < k2

Пример параметрического нелинейного закона:

u = k (t [°C]; h [м]; G [кг]) x

.

Пример оптимизирующего нелинейного закона:

u = k (min(CO2); max(КПД)) x .

Пропорциональное регулирование

Пропорциональный закон регулирования имеет вид:

u(t) = Wрег(p) x(t) = k1x(t) ,

тогда в разомкнутом состоянии система будет характеризоваться ПФ:

W(p) = Wрег(p) Wo(p) = k1Wo(p) .

Рассмотрим уравнение ошибки:

В установившемся режиме p®0 (все производные равны нулю); Wo(p)®ko;

W(p)®k1ko=k;

где k - контурный коэффициент усиления разомкнутой системы (при Wос(p)=1).

Резюме: P-регулирование позволяет уменьшить установившуюся (статическую) ошибку, но только в 1+k раз, поэтому регулирование будет статическим. Т.е. при любом k xуст№0.

Пространство состояний

Рабочие файлы: [ABCD.vsm] [ABCD-ПФ и W(jw)]

Пространство состояний (ABCD-форма)

Матричная форма записи системы ДУ САР адаптированная для теории управления путем выделения из формы Коши алгебраических уравнений связывающих внутренние координаты САР с выходной(ыми). Применяется для описания САР большого порядка, как правило, с несколькими входами / выходами и с перекрестными связями.

Изображенная на рисунке блок-схема позволяет решить систему ДУ представленную в форме "Пространства состояний":

(3)

u' = A u + B x

y = C u + D x

где:

xmx 1 - вектор входных переменных;

yk x 1 - вектор выходных переменных;

un x 1 - вектор переменных состояния (фазовых координат системы);

An x n - матрица коэффициентов системы;

Bn x m - матрица входных коэффициентов (матрица управления);

Ck x n - матрица выходных коэффициентов;

Dk x m - матрица коэффициентов пропорциональных каналов (матрица компенсации);

n - порядок системы; m - кол-во входов; k - кол-во выходов (m<n).

О форме "Пространство состояний":

Это вторая по частоте применений форма записи ДУ в ТАУ. Применяется реже, чем в 5% случаев.

Признана стандартом для программ математического моделирования VisSim, Simulink, и т.д., однако в большинстве случаев реализована в SISO-форме (с одним входом и одним выходом). Моделирующие программы для выполнения анализа (символьного или частотного) сводят любую модель пользователя к пространству состояний, заполняя в ходе первых шагов симуляции коэффициенты ABCD-матриц.

Как правило, используется для построения моделей тех больших не поддающихся модуляризации, но не сложных систем, описание которых оптимально в матричной форме (таких мало). Для записи уравнений используются такие методы как: "Метод контурных токов", "Метод узловых потенциалов", - а так же их эквиваленты для других энергетических доменов (гидравлического, теплового, механического, ...).

Матричное описание строго формализовано, и не требует понимания физической природы системы. Так же структура модели в "пространстве состояний" не позволяет разобраться во внутренней природе системы. Если эта форма записи ДУ применена обосновано, то модель, скорее всего, будет истинной.

Рабочая программа дисциплины ТАУ

Для написания собственной рабочей программы Вам следует сохранить архив vissim.nm.ru/rp_tau.zip на своем диске, разархивировать содержащийся в нем документ программы MS Word. Внести требуемые изменения и распечатать.

Предлагаемый макет программы не содержит информацию для служебного пользования (билеты к экзамену, и пр.), поскольку предполагается передача учебно-методического комплекса в данной комплектации студентам.

Расчет промежуточных переменных

A = sqrt[ 10^(dBgain/20) ] = = 10^(dBgain/40) (только для полософормирующих фильтров)

omega = 2*pi*frequency/sampleRate

sin = sin(omega) cos = cos(omega)

alpha = sin/(2*Q) = (если задана Q) = sin*sinh[ ln(2)/2 * bandwidth * omega/sin ] (если задана полоса)

Отношение между шириной полосы и Q: 1/Q = 2*sinh[ln(2)/2*bandwidth*omega/sin] (для ЦФ на основе БЛП) or 1/Q = 2*sinh[ln(2)/2*bandwidth] (для аналогового прототипа)

beta = sqrt(A)/Q = (только для фильтров-ступенек) = sqrt(A)*sqrt[ (A + 1/A)*(1/S - 1) + 2 ] (если задан наклон горки) = sqrt[ (A^2 + 1)/S - (A-1)^2 ]

Отношение между наклоном и Q: 1/Q = sqrt[(A + 1/A)*(1/S - 1) + 2]

ФНЧ: H(s) = 1 / (s^2 + s/Q + 1)

b0 = (1 - cos)/2 b1 = 1 - cos b2 = (1 - cos)/2 a0 = 1 + alpha a1 = -2*cos a2 = 1 - alpha

ФВЧ: H(s) = s^2 / (s^2 + s/Q + 1)

b0 = (1 + cos)/2 b1 = -(1 + cos) b2 = (1 + cos)/2 a0 = 1 + alpha a1 = -2*cos a2 = 1 - alpha

ПФ: H(s) = s / (s^2 + s/Q + 1) (пик АЧХ = Q)

b0 = sin/2 = Q*alpha b1 = 0 b2 = -sin/2 = -Q*alpha a0 = 1 + alpha a1 = -2*cos a2 = 1 - alpha

ПФ: H(s) = (s/Q) / (s^2 + s/Q + 1) (пик АЧХ = 0 dB)

b0 = alpha b1 = 0 b2 = -alpha a0 = 1 + alpha a1 = -2*cos a2 = 1 - alpha

Режекторный фильтр или фильтр - пробка: H(s) = (s^2 + 1) / (s^2 + s/Q + 1)

b0 = 1 b1 = -2*cos b2 = 1 a0 = 1 + alpha a1 = -2*cos a2 = 1 - alpha

Фазовращающий фильтр: H(s) = (s^2 - s/Q + 1) / (s^2 + s/Q + 1)

b0 = 1 - alpha b1 = -2*cos b2 = 1 + alpha a0 = 1 + alpha a1 = -2*cos a2 = 1 - alpha

Полософормирующий фильтр (для эквалайзеров): H(s) = (s^2 + s*(A/Q) + 1) / (s^2 + s/(A*Q) + 1)

b0 = 1 + alpha*A b1 = -2*cos b2 = 1 - alpha*A a0 = 1 + alpha/A a1 = -2*cos a2 = 1 - alpha/A

Фильтр - НЧ-ступень-лестница: H(s) = A * (s^2 + (sqrt(A)/Q)*s + A) / (A*s^2 + (sqrt(A)/Q)*s + 1)

b0 = A*[ (A+1) - (A-1)*cos + beta*sin ] b1 = 2*A*[ (A-1) - (A+1)*cos ] b2 = A*[ (A+1) - (A-1)*cos - beta*sin ] a0 = (A+1) + (A-1)*cos + beta*sin a1 = -2*[ (A-1) + (A+1)*cos ] a2 = (A+1) + (A-1)*cos - beta*sin

Фильтр - ВЧ-ступень-лестница: H(s) = A * (A*s^2 + (sqrt(A)/Q)*s + 1) / (s^2 + (sqrt(A)/Q)*s + A)

b0 = A*[ (A+1) + (A-1)*cos + beta*sin ] b1 = -2*A*[ (A-1) + (A+1)*cos ] b2 = A*[ (A+1) + (A-1)*cos - beta*sin ] a0 = (A+1) - (A-1)*cos + beta*sin a1 = 2*[ (A-1) - (A+1)*cos ] a2 = (A+1) - (A-1)*cos - beta*sin

Распределяющий (материю) узел

Основу распределяющего узла составляет обслуживаемый неявным решателем трехвыводной сумматор, математическое уравнение которого соответствует постулату о сохранении материи (например, это может быть I закон Кирхгофа). Соблюдение этого постулата обеспечивает датчик неявного решателя (блок constraint) на выходе сумматора. Перераспределение же потоков материи I2 и I3 контролирует второй датчик неявного решателя, фиксирующий разность потенциалов

j2 и j3. Если (j2-j3)> 0, то баланс в цепи может быть найден при уменьшении потока I2 и увеличении I3. Если (j2-j3) < 0, то неявному решателю потребуется увеличить поток I2 и уменьшить I3. (Изменения потоков материи приводят к тому, что элементы ненаправленного графа меняют значения соответствующих потенциалов). Таким образом, принцип работы узла состоит в том, чтобы распределить поток материи I1 на потоки I2

и I3 так, чтобы соблюдалось равенство потенциалов

j2 и j3 (после нахождения баланса цепи потенциал j1 будет равен потенциалам j2 и j3).

Разложение математического описания модели САР в степенной ряд

Рабочие файлы: [ABCD ®

с1с2с3]

Разложение математического описания модели в степенной ряд

Процедура разложения в степенной ряд системы дифференциальных уравнений САР решенной относительно требуемой координаты. Таким образом результат процедуры – первые коэффициенты разложения (коэффициенты ошибок, или коэффициенты отклика) – получается в результате трансформации либо ABCD-матрицы коэффициентов, либо коэффициентов числителя и знаменателя ПФ.

Известно, что например коэффициенты ошибок связывают коэффициенты разложения входного сигнала g(t) в ряд Тейлора с соответствующими составляющими ошибки x(t) в установившемся режиме движения:

x(t) = c0 g(t) + c1 g'(t) / 1! + c2 g''(t) / 2! + c3 g'''(t) / 3! + ...

Этот факт положен в основу техники разложения математического описания модели в степенной ряд. Идея заключена в том, что библиотека анализа моделирующей программы, за один процедурный шаг, балансирует модель в одном из возможных состояний установившихся режимов движения (неподвижное ненулевое состояние, движение с постоянной скоростью, и т.д.). Далее, измерив значения двух координат (относительно которых требуется выполнить разложение), вычисляет их отношение, находя тем самым соответствующий коэффициент искомого ряда.

В общем виде математическое обоснование техники разложения математического описания модели САР в степенной ряд объемно и опирается на аппарат матричных исчислений (лишь матричное описание позволяет учесть любые возможные взаимосвязи между координатами модели). Поэтому опишем лишь алгоритм, согласно которому функционируют соответствующая процедура библиотеки анализа моделирующих программ:

Пользователь указывает две координаты линейной непрерывной модели: вход и выход, – относительно которых требуется выполнить разложение и активирует соответствующую процедуру анализа.

Библиотека анализа замещает все интеграторы модели специальной блок-схемой, изображенной на рисунке справа. К указанному пользователем входу библиотека подключает генератор импульса единичной амплитуды, и подготавливается к измерениям выходной координаты (начиная с этого шага алгоритма допустимо, чтобы программы не использовали графический интерфейс, т.е.
скрывали технические подробности от пользователя).

Далее, библиотека анализа инициирует процесс спец- симуляции модели. На каждом шаге выполняется измерение одного коэффициента разложения (в силу особенностей задающего сигнала значение выходной координаты равно коэффициенту разложения).

Достоинство описанного алгоритма заключается в том, что после упомянутой подстановки, величина шага симуляции моделирующей программы не имеет влияния на результат разложения. Однако процедура балансировки модели требует решения системы линейных алгебраических уравнений, порядок которой равен порядку исследуемой САР.

Если исходной информацией к разложению будут являться не ABCD-матрицы коэффициентов, а коэффициенты числителя и знаменателя ПФ разомкнутой САР, то балансировка модели в установившихся режимах движения может быть упрощена, поскольку итерационному решателю моделирующей программы достаточно прорешивать алгебраическое уравнение лишь первого порядка. Требуемые в этом случае трансформации исходной модели и результат разложения показаны на рисунке.

Размыкание систем с запаздыванием

Большинство методов исследования устойчивости или качества систем в качестве входной информации используют ПФ системы для разомкнутого состояния W(s). Звено чистого запаздывания является нелинейным элементом, и затрудняет как аналитический анализ систем, так и машинный (программы математического моделирования не могут выполнять функции анализа для систем с нелинейными элементами). Поэтому либо используют линеаризованные аппроксиматоры звена чистого запаздывания, либо размыкают систему в той ветви, которая содержит звено чистого запаздывания, дабы ПФ имела вид: W(s)= Wo(s) ґ e-ts, где Wo(s) - ПФ части системы без запаздывания.

Рассмотрим и разомкнем системы с основными вариантами включения звена чистого запаздывания - последовательным, параллельным и в цепи ОС:

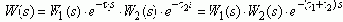
Если звенья чистого запаздывания имеются в разных ветвях структурной схемы, то для исследований используют их аппроксиматоры и машинные методы анализа.

Разностные уравнения

Аналогом ДУ для импульсной системы является уравнение в конечных разностях или разностное уравнение (РУ):

b0Сmy[n] + b1Сm-1y[n] + ... + bm y[n] = f [n],

(оно может быть составлено и в прямых разностях). Если раскрыть разности, то уравнение будет иметь вид:

(1)

a0 y[n] + a1

y[n-1] + ... + am y[n-m] = f [n],

где:

am-k =n=0kе (-1)m-k bn Cm-nk-n ;

Cm-nk-n = (m-n)! / [ (k-n)! (m-k)! ] .

РУ легко машинизируются и для их расчета можно составлять рекуррентный алгоритм.

Учтем запаздывание передаточной функцией звена чистого запаздывания и вынесем теперь уже изображение дискретной последовательности y[n]

в уравнении (1) за скобку:

(a0 + a1e-Ts

+ ... + ame-mTs) Y *[s] = F *[s],

введем обозначение z = eTs и перепишем уравнение:

(a0 + a1 z -1

+ ... + am z -m) Y [z] = F [z].

Решая для него ХУ (левая часть приравненная к нулю) можно получить "Общее решение" - т.е. переходную составляющую:

y [n] = С1 z1n

+ С2 z2n + ... +  Сm zmn ,

где: z1, z2, ..., zm

- корни ХУ; а Ci - произвольные постоянные.

Вид решения ХУ определяет условие устойчивости для систем, описанных с помощью РУ:

| zi | < 1.

Внутренняя структурная схема реактивных элементов

Внутренняя структурная схема реактивных элементов принципиально не отличается от структурной схемы безинерционного потребителя энергии. Различие состоит лишь в способе расчета создаваемого потоком падения напряжения. В частности, реактивный элемент индуктивного характера должен обеспечивать в заданном масштабе (L) тем большую разность потенциалов, чем больше скорость изменения протекающего по нему потока (di/dt). Это падение напряжения вычисляется с помощью блоков unknown (неизвестная) и constraint (баланс_в_нуле) следующим образом (см. блок-схему). На каждом шаге симуляции неявный решатель моделирующей программы с помощью итерационного процесса подбирает такое выходное значение блока unknown, чтобы на входе блока constraint было нулевое значение. Однако интегратор – это блок обладающий эффектом памяти – он разрывает сигнальную цепь – сигнал на его входе на данном шаге симуляции ни как не определяет выходное значение (сигнал на входе интегратора определяет его выходное значение лишь на следующем, в данный момент еще не вычисляемом шаге симуляции). Баланс на входе блока constraint подбирается через цепь верхнего разъема, и ту схему, к которой элемент подключен. Т.е. фактически подбирается не выходное значение интегратора, а поток, протекающий по элементу. Если баланс будет вычислен, то значение сигнала на входе интегратора будет равно производной потока, а на входе делителя – искомому напряжению.



Приведенное описание принципа работы блок-схемы позволяет легко понять, что установка начального условия на интеграторе (Initial Condition), эквивалентна определению величины начального потока материи по элементу.

Реактивный элемент емкостного характера должен

Реактивный элемент емкостного характера должен обеспечивать в заданном масштабе (1/С) разность потенциалов пропорциональную интегралу протекающего по нему потока i, что и обеспечивается блок-схемой показанной на рисунке.



Установка начального условия на интеграторе данной блок-схемы эквивалентна определению величины начального падения напряжения на элементе.

Регистрация документа на Вашем компьютере

Если Вы часто пользуетесь этим документом, то постоянная активация счетчика статистики в документе будет мешать вам. Вы можете получить у автора пароль, для деактивации счетчика на полгода. Заполните и отправьте форму:

ФИО:	*
Должность:
Научное звание:
Организация (вуз):	*
Город:	*
Область:	*
Укажите сайт, откуда вы скачали этот документ:
http://
Какими программами для моделирования
вы пользуетесь?
Сообщать вам об обновлениях?

Если пароль получен вами, то введите его в эту строку:

Срок действия пароля определен периодом публикации новой версии документа. Если срок истек, и счетчики вновь начали работать, то рекомендуется обновить версию документа. Так же допустимо отключить счетчики повторным вводом пароля на очередные полгода.

Регулирование с использованием производных

Рабочие файлы: [Шум дифференцирования]

Регулирование с использованием одного канала, чувствительного к производной сигнала не имеет самостоятельного значения, т.к. сигнал управления:

u(t) = Wрег(p) x(t) = k4 p x(t) ,

будет равен нулю при p®0 (т.е. в установившемся режиме). Поэтому обязательно наличие параллельного либо P, либо I-канала, а чаще обоих:

u(t) = (k1 + k2/p

+ k4 p) x(t) .

В таком варианте регулятора управляющее воздействие будет образовываться даже когда x(t)=0, но dx/dt№0. Т.е. наличие параллельного D-канала в регуляторе повышает быстродействие системы и снижает ошибки в динамике.

Сегодня техническая реализация регуляторов, чувствительных к производным более высоких порядков, затруднена.

Рекомендации к использованию библиотеки элементов

Рабочие файлы: [Элементы] [RLC схема] [Схема электрическая]

[Ее граф в VisSim'е]

Описанные модели элементов ненаправленного графа являются идеализированными, т.е. имеют стремящиеся к нулю внутренние сопротивления, обладают высокой добротностью, или совершенно не имеют инерционных свойств, как то и требуется для схем замещений. Отсюда следует, что неправильно составленный ненаправленный граф может привести к перегрузке мантиссы решателей. Приведем примеры для электрического энергетического домена:

Замыкание заряженного конденсатора или источника электродвижущей силы на нулевое сопротивление или конденсатор с другим падением напряжения.

Размыкание индуктивной катушки с электрическим током без подключения шунтирующего резистора.

Другой причиной проблем с решателями могут послужить элементы, установленные на рабочее поле, но не подключенные к графу. Далеко не у всех моделирующих программ неявные решатели умеют находить и исключать из расчетов те датчики нулевого баланса и блоки неизвестная, которые не связаны функциональной зависимостью (т.е. не подключены). По той же причине не следует создавать не связанные, хотя бы потенциально, энергетические цепи, поскольку в этом случае, так же образуются независимые области итерационного подбора.

Не следует так же забывать, что итерационный поиск баланса для десятков, а то и сотен координат (переменных) энергетических цепей выполняется на каждом шаге симуляции. Очевидно, что итерационный процесс будет тем короче, чем меньше приращения значений координат. Отсюда следует рекомендация отказываться, в критических случаях, от задающих генераторов, чьи выходные последовательности имеют разрывы: меандр, пила, и т.д. (Пропустите сигналы соответствующих источников опорного напряжения, через апериодические звенья первого порядка с малой постоянной времени).

Решатели моделирующих программ

Рабочие файлы: [Метод Ньютона] [Метод секущих] [Формулы] [СЛАУ] [СНАУ] [ДСНАУ]

Явный решатель моделирующей программы

Это библиотека классических подпрограмм (функций), которые реализуют операцию интегрирования. (Дискретные квази-аналоги интеграторов используются для решения дифференциальных уравнений).

Неявный (итерационный) решатель моделирующей программы

Это библиотека классических подпрограмм, которые предназначены для решения алгебраических уравнений путем итерационного подбора независимых переменных.

Оптимизирующий решатель моделирующей программы

Это разновидность неявного решателя, которая предназначена для минимизации значения функции в процессе итерационного подбора ее независимых переменных.

На рис. показана техника подключения неявного решателя (блоков

unknown и constraint – неизвестная

и нулевой_баланс) к алгебраическому полиному с целью поиска корней уравнения. На каждом шаге симуляции неявный решатель, в итерационном процессе, подбирает такое значение на выходе блока неизвестная (этот блок, по сути, является генератором сигнала), которое, будучи подставлено в полином обнулит его. За фактом обнуления следит датчик решателя – блок нулевой_баланс. Если инициировать решатель (блок неизвестная) разными начальными значениями, то можно найти оба корня.

Решетчатые функции

Рабочие файлы: [z_sin.vsm]

Решетчатые функции2 определены только в дискретные моменты времени [nT] (сокращенно [n]), и формируются из непрерывных функций 1: f [nT] = f (t)

при t=nT. Рассматривают так же смещенные решетчатые функции (последовательность 3): f [n, e] = f (t)

при t=(n+e)T, где

e - относительное смещение, eО[0..1).

Основная огибающая может быть получена, как результат решения ДУ наименьшего порядка и должна содержать гармоники наименьшей частоты.

В статье описана модульная структура

В статье описана модульная структура программ математического моделирования динамических систем. К основными компонентам отнесены: редактор векторной графики, СУБД, математическое ядро, серверы визуализации и Online-воздействий.
Представлен обзор программных решений, которые, с высокой степенью вероятности, положены в основу математических ядер моделирующих программ с поточной моделью управления. Предпринята попытка сформировать пользовательский спрос на математические ядра выполненные в виде COM-серверов.
Продемонстрирована возможность интеграции математических ядер разных производителей с редактором векторной графики Visio. Указано на неустойчивость рынка моделирующих программ, по причине наличия у корпорации Microsoft трех из четырех технологий, необходимых для выхода на этот рынок и его захвата.
Сформулированы задачи, которые должны решать модули стыковки основных компонент программ математического моделирования динамических систем. Предложена схема данных и XML-схема хранилища направленного графа (рисунка блок-схемы), что может вызвать интерес у разработчиков.

Сценарий изменения методики преподавания "Теоретических основ цепей" и обзор затруднений

Показанные противоречия, бесспорно, требуют изменений в методике преподавания. Перед педагогами стоит серьезная задача. Согласно стратегическим взглядам Министерства образования требуется внедрить в процесс обучения компьютеры, и, за счет каких-то их мультимедийных, интерактивно-волшебных возможностей сократить количество лекционных занятий, увеличив при этом долю самостоятельной работы студентов.

"Теоретические основы цепей" всегда были самыми сложными дисциплинами. "Программы-калькуляторы" ни коем образом не позволят педагогу подготовить учебный материал в более наглядной и доступной форме, дабы его можно было вынести в часы самостоятельной работы студента. Поэтому опора на такие программы как Matcad, Mathematica, Maple; плюс стремление педагогов (впрочем, согласно требованиям стандартов Министерства образования) сохранить тематическое содержимое приводит к разрушению этих фундаментальных дисциплин.

Оценка всех возможных вариантов ужатий, сокращений, и интерактивно-волшебных возможностей компьютеров дает лишь один максимально безвредный сценарий изменения методики преподавания "теоретических основ цепей":

Исключение из программ дисциплин всех тем, связанных с изучением особенностей подходов к решению задач первых трех уровней и обучение решению этих же задач с применением математического аппарата адекватного по уровню сложности задачам четвертого уровня.

Использование специализированных решателей для моделирования динамических процессов (DyMoLa, Dynast, Multisim, Micro-Cap; VisSim, MBTY, MVS, Simulink).

Подобный переход не просто труден, а труден существенно. Так повальная гуманитаризация высшего технического образования в России привела к тому, что вследствие сокращения часов неспециалисты в итоге обучения знакомы с задачами расчета цепей преобразования энергий лишь первых двух уровней сложности. Предлагается же сразу перейти к четвертому уровню. Кроме того, крайне желательно, дабы на момент перехода были одновременно модифицированы рабочие программы нескольких дисциплин: физики, ТОЭ, гидропневмоавтоматики, механики линейных и ротационных перемещений, теплотехники, основ моделирования систем (или математики), а так же целого веера дисциплин стоящих за теоретическими основами каждого энергетического домена.

Отдельная и существенная проблема заключается в несерьезном отношении российского общества, как к моделированию технических систем, так и к покупке соответствующего программного обеспечения. Вот факты: В России лишь два коллектива разрабатывают программы, которые со временем, если не разорятся, будут поддерживать технологию мультидоменного физического моделирования с применением ненаправленных графов (MBTY и MVS). Разработчики тех же программ утверждают, что Российские вузы не покупают их продукт. При этом факт воровства программы MBTY работниками вышей школы, с попыткой дальнейшего коммерческого использования был зафиксирован на территории Казахстана в начале 2003 года. Промышленность России, за исключением атомной, вообще не интересуется подобными программами.

Чуть меньшим препятствием является стремление разработчиков программ для мультидоменного моделирования, таких как Multisim (EWB), Dynast, 20-sim, ITI-SIM, Simplorer и DyMoLa, скрыть принципы их функционирования. Как любое непознанное, это вызывает недоверие у преподавателей к данным программам и порождает сомнения в возможности отказа от большинства формализованных методов расчета цепей. Автор высказывает надежду, что данное пособие развеет часть этих сомнений.

Шлюз Visio2SimKernel

Если проанализировать вводную информацию по графическому интерфейсу моделирующих программ, то становятся очевидны задачи, возлагаемые на шлюз Visio2SimKernel:

Контроль над процессом создания рисунка блок-схемы или же схемы физической принципиальной (техника выполнения рисунка блок-схемы отличается от техники выполнения чертежа гайки и возможны специфические облегчения некоторых графических процедур; также требуется контролировать соблюдение некоторых правил создания блок-схем, например отсутствие коротких замыканий выходов и др.).

Дешифровка рисунка направленного графа (блок-схемы) и трансформация информации в программирующие математическое ядро инструкции (см. листинг2).

Трансформация ненаправленного графа (схемы физической принципиальной), путем перебора уточняющих коммутаций, в виртуальный (неначерченный) направленный, точнее би- или сонаправленный граф.

Дешифровка графических образов, отвечающих за программирование потока(ов), и их трансформация в инструкции переключений математического ядра, а лучше ядер, каждое из которых может отвечать за свой поток, т.е. за свой фрагмент модели.

Дешифровка графических образов, отвечающих за синхронизацию потоков (ядер).

Контроль над процессом симуляции модели; управление процессами визуализации результатов и синхронизации Online воздействий (фактически это еще один шлюз).

В случае использования Visio [8], в качестве графического интерфейса, модульная структура моделирующей программы, изображенная на рис. 1, может быть сокращена. Достаточно оставить Visio, COM-сервер математического ядра, а так же серверы визуализации и Online воздействий. Тому способствуют следующие благоприятные моменты. Последние версии Visio ориентированны на сохранение рисунков в файлах с XML разметкой. Роль библиотеки шаблонов блоков SimKernel_Lib.xml может выполнять определяемая пользователем библиотека графических примитивов Visio (vss-файл). Причем, последние могут иметь переопределяемые пользователем параметры, которые сохраняются в файле рисунка.
Объектная модель Visio имеет разделённые коллекции для библиотечных графических примитивов (в нашем случае это блоки), для линий связи, и для коннектеров, что упрощает написание шлюза.

Для математических ядер разных производителей шлюз будет отличаться лишь синтаксисом интерфейсов (табл. 2), который должны уточнить сами производители. Реализация первых двух задач, возложенных на шлюз Visio2SimKernel весьма проста (программа на VB не превышает двух сотен строк). Данной, сокращенной версии шлюза достаточно, дабы перекрыть возможности графических интерфейсов таких программ как Simulink, VisSim, MBTY, т.е. закрыть потребности техники структурного моделирования.

Таким образом, производителю математического ядра достаточно поставить: графическую библиотеку блоков, собственный шлюз (Visio2VisSim, Visio2Simulink, Visio2MBTY) и настроенный шаблон документа Visio, дабы пользователь мог использовать его для создания новых моделей. Шлюз может быть оформлен либо в виде вмонтированного в шаблон документа макроса, либо в виде расширений: add-in'а — для контроля над процессом создания рисунка через механизм событий,  и add-on'а — для исполнения процедур дешифраций рисунка, программирования математического ядра и управления серверами визуализации и Online-воздействий.

Завершая обзор шлюза, надо отметить, что благодаря гибкости графического интерфейса на основе редакторов векторной графики, впервые у конечного пользователя моделирующих программ появится возможность решить задачу трансформации ненаправленного графа в граф направленный независимо от производителя. А это означает, что техника мультидоменного физического моделирования сделает громадный рывок вперед, поскольку перестанет быть ноу-хау нескольких фирм (см. программы: Dynast, 20-sim, Dymola, Simplorer, ITI-sim, Micro-Cap, Pspice, Multisim).

Сигналы задания для типовых режимов движения, их модели и изображения по Карсону-Хевисайду

На рис. показаны режимы: ненулевого, неподвижного положения координаты; движение с постоянной скоростью; движение с постоянным ускорением. Легко понять, что перемещение координаты с постоянной скоростью легко получить интегрированием постоянного сигнала, а для получения координаты движущейся с постоянным ускорением необходимо интегрировать координату перемещающуюся с постоянной скоростью. Заменив операцию интегрирования оператором, получим изображения по Карсону-Хевисайду.

Символьный анализ математического описания моделей

Символьные преобразования математического описания моделей

Те или иные алгоритмические процедуры, в результате исполнения которых моделирующая программа трансформирует математическое описание модели к желаемому виду (вплоть до изменения её структуры). В список основных символьных преобразований (чье наличие обязательно для библиотек анализа моделирующих программам) входят: билинейное преобразование, поиск корней алгебраических полиномов и разложение в степенной ряд (получение коэффициентов ошибок).

Синтез параметрических САР

При синтезе САР на ЭВМ так же используют "замораживание" коэффициентов, и, если во всем рабочем интервале времени качество САР оказывается приемлемым, ее считают работоспособной.

Во многих случаях удается выделить одно звено первого или второго порядков с var-параметром. Тогда возможно осуществить синтез САР расчетным путем.

При синтезе следует стремиться максимально точно определить законы изменения параметров и не ограничиваться диапазонами. Так для случая 2 изменений var-параметров, согласно "D"-разбиению вероятность сохранения устойчивости существенно больше.

Синтез САР

Синтез системы

Направленный расчет, имеющий конечной целью отыскание: 1)рациональной структуры системы и 2) установление оптимальных величин параметров отдельных звеньев.

При множестве возможных решений, должен быть выбран критерий оптимизации - цена, точность, надежность, быстродействие, затраты энергии ...

При инженерном синтезе ставятся задачи:

Достижение требуемой точности.

Обеспечение приемлемого характера переходных процессов (задача демпфирования).

Решение первой задачи заключено в выборе средств повышающих точность системы (усилительных, изодромных блоков; каналов КУ; не 1ОС), т.е. фактически вида регулирования.

Решение второй задачи заключено в выборе оптимальных корректирующих средств.

Системы с переменными параметрами

Система линейная с переменными параметрами

Линейной системой с переменными (var) параметрами называется такая, движение которой описывается ДУ с переменными во времени коэффициентами:

где воздействие f может быть и задающим - g(t).

Те. ПФ подобной системы параметрическая, например:

W(s, t ) =		Y(s, t)	=	K(t)...
X(s, t)	(1+T1s)(1+T2(t)s)...

где: K(t), T2(t) - зависящие от времени функции.

Системы с запаздыванием

Система линейная с запаздыванием

Линейной системой с запаздыванием называется такая, которая содержит в своей структуре хотябы одно звено, в котором есть неизменное запаздывание во времени

t изменения выходной координаты после начала изменения входной.

(1)

Tdy/dt + y = K x(t) .

Уравнение соответствующего звена с запаздыванием t

будет иметь вид:

(2)

T dy/dt + y = K x(t-t) .

Оно называется дифференциально-разностным.

Обозначим x*(t) = x(t-t), тогда уравнение (2) запишется в обыкновенном виде:

(3)

T dy/dt + y = K x*(t) .

Следовательно его переходная характеристика соответствует апериодическому звену (рис. 1в), но задержана на t с, что определено задержкой воздействия x*(t) (рис. 1б).

Резюме:

Временная характеристика любого звена с запаздыванием будет такая же, как у соответствующего обыкновенного звена, но только сдвинута по оси времени вправо на величину t.

Величину запаздывания t в звене можно определить экспериментально, путем снятия временной характеристики.

Снижение ошибки от сигнала задания введением сигнала КУ на входе регулятора

Рабочие файлы: [пример]

где: Fэк(s) - эквивалентная ПФ для данной системы.

Fx.эк(s) = 1- Fэк(s)).

Разложим 1/W(s) в ряд по возрастающим степеням оператора, тогда: j(s)=a0+t1s+t22s2+t33s3+..., т.е. ПФ j(s) должна состоять из масштабирующего (a0<<1) и дифференцирующих звеньев (t1s,

t22s2, t33s3, ...).

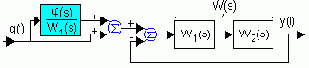
На рисунке показаны структурные схемы исходной и преобразованной системы. Для последней легко записать уравнение движения:

Fx.эк(s) = 1- Fэк(s)).

Снижение ошибки от возмущающего сигнала применением КУ

Достоинство КУ:

Поскольку знаменатели функций F(s) (исходной) и Fэк(s) равны, введение j(s) не меняет характеристического уравнения системы, следовательно, не нарушаются условия устойчивости.

Недостатки КУ:

Требуется точная подстройка коэффициентов ПФ j(s).

При изменении параметров W(s) появляются ошибки.

Практическая реализация дифференцирующих звеньев высокого порядка затруднительна.

Соглашения, закрепленные договором

Договор не может ущемить ни одного из прав Автора на собственное Произведение.

Автор передает фирме Visual Solutions Inc право распространения своего Произведения совместно с производимой фирмой программой VisSim.

Автор сохраняет за собой право независимого распространения своего Произведения.

Фирма Visual Solutions Inc обязуется распространять Произведение Автора на правах "Свободной информации" и не ущемлять следующих прав пользователей:

Право запускать Произведение в любых целях.

Право изучать работу документа (Произведения) и адаптировать его собственным нуждам.

Право распространять копии Произведения1.

Право улучшать Произведение и публиковать версии на правах

"Свободной информации".

Договор вступает в силу с момента опубликования Автором версии

Произведения, содержащей текст договора и имеющей цифровую подпись2

Автора.

1) Право пользователя распространять копии Произведения

(т.е. право распространять файл tau_knv.chm) не включает в себя право распространять копии программы VisSim. Незаконное распространение, или копирование программы VisSim запрещено.

2) Публичный ключ Автора (файл KNV.ASC) можно найти в директории SIGNS после распаковки файла Произведения. Цифровая подпись индивидуальна для каждой версии Произведения и распространяется совместно с ним (файл tau_knv.sig).

Способы введения корректирующих звеньев

Результирующие ПФ:

Формулы эквивалентных переходов:

Показания к применению:

- последовательная коррекция - электрические цепи с немодулированными сигналами (легка в проектировании);

 - параллельная коррекция - необходимость ВЧ-шунтирования инерционных звеньев;

 - коррекция локальной ОС - необходимость уменьшения нелинейностей, дрейфа параметров или суммы постоянных времени (проста в реализации).

Суть линеаризации

Пусть нелинейное динамическое уравнение звена имеет вид:

F(x1, x2, x2', y, y', y'', y''') = j( f, f') .

Тогда уравнение установившегося состояния, всилу равенства нулю всех производных, имеет вид:

Fo(x1o, x2o, 0, yo, 0, 0, 0) =

j( f o, 0) .

Перейдем к уравнению динамики для отклонений, выполнив подстановки:

x1

= x1o+Dx1(t),   x2 = x2o+Dx2(t),    x2' = Dx2'(t),

y = yo+Dy(t),    y' = Dy'(t),    y'' = Dy''(t),    y''' = Dy'''(t);

и разложив функцию F в ряд:

.

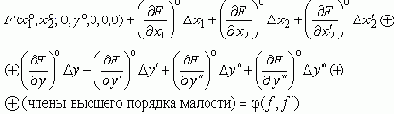
Завершая линеаризацию, вычтем из левой и правой части уравнение установившегося состояния:

(*)

.

Сведения об источнике обновленных версий документа

Обновленные версии данного цифрового документа доступны на сайте "VisSim в России". Если при загрузке с сайта возникают технические затруднения, то для их решения можно связаться с автором (адрес электронной почты: klinacherv_nv@mail.ru). При возможных изменениях в адресах рекомендуется воспользоваться поисковыми системами, используя ключевые слова: VisSim, симуляция движения, моделирование, Nikolay Klinachyov.

Свойства годографа Михайлова

Годограф всегда спиралевиден.

При w=0, будетy=0, следовательно годограф начинается с точки на оси "+1".

Поскольку при w®Ґ K(jw)®0 (нет безинерционных систем), годограф уходит в бесконечность.

При четном n, годограф стремится к Ґ параллельно оси "+1"; при нечетном n, годограф стремится к

Ґ параллельно оси "+j".

Свойства годографа Найквиста

При w®Ґ годограф W(jw)®0, т.к. нет безинерционных систем.

Годограф статических САР начинается из точки на вещественной оси.

Для положительных и отрицательных частот годографы зеркально симметричны относительно оси "+1".

Наличие корней на границе устойчивости приводит к устремлению годографа в

Ґ и приращению его фазы на -1800.

Технические аспекты

Учебно-методический комплекс выполнен в соответствии со стандартом Windows-HTML-справки. Он представляет собой один файл, в котором заархивированы html-страницы, рисунки и необходимые скрипты. Файл пособия автоматически распознается и запускается операционной системой Windows 98 (NT, 2000), точнее браузером MSIE версии не ниже 4.0. Пользователям Windows 95 (NT) дополнительно следует установить Windows-HTML-справку. Для чего следует найти файл hhupd.exe (733 KB). Там же, или в секторе "download" сайта фирмы Microsoft, вы можете скачать программу HTML Help Workshop (файл htmlhelp.exe (4 MB)). Используя ее, Вы можете декомпилировать пособие для запуска в браузере Netscape или для создания собственного на основе этого образца. Программа HTML Help Workshop также содержит утилиту для создания gif-файлов с изображениями необходимых вам фрагментов экрана. Для корректной цветопередачи при создании gif-файлов активируйте цветовое разрешение дисплея в 256 цветов. Пособие так же полностью функционально и запускается браузером MSIE, если в адресной строке набрать:

mk:@MSITStore:C:\tau_knv.chm::/index.htm - где C:\

- путь к файлу tau_knv.chm.

Технологии функционирования моделирующих программ

Каждая из программ математического моделирования динамических систем основана на одной из двух технологий:

Первая технология предполагает использование поточной модели управления

при выполнении математических преобразований (функций) составляющих модель.

Вторая технология предполагает представление модели в виде текстовой записи системы уравнений, которую решатели моделирующих программ обрабатывают в пакетном режиме.

Поточная модель управления (Data Flow)

Модель программирования, в которой инструкции, процедуры или функции выполняются только тогда, когда все входные данные (т.е. параметры и аргументы) готовы.

Все потенциальные возможности программ с поточной моделью управления можно оценить, ознакомившись с программным комплексом LabVIEW (это не моделирующая программа, а лишь блестящий пример возможностей технологии). Вторая технология наиболее понятно и открыто представлена в программе Dynast.

Тематический план лекционных занятий

Введение. Классификация САР 1. Составление исходных ДУ САР 2. Описание САР в частотном домене 3. Типовые динамические звенья 4. Принципы и законы регулирования 5. Устойчивость САР 6. Оценка качества регулирования 7. Повышение точности САР 8. Коррекция САР 9. Синтез САР 10. Системы с переменными параметрами 11. Системы с запаздыванием 12. Системы импульсные 13. Системы цифровые Литература

Типовая структура импульсной системы. Понятие об импульсном фильтре

Если время замкнутого состояния ключа мало, то сигнал на его выходе можно заменить последовательностью дельта-функций x*[nT], с площадью x[nT], т.е: x*[nT]= x[nT] d(t-nT).

В таком случае реакция непрерывной части Wo(s) - это суперпозиция весовых функций w(t), которую можно рассматривать и как непрерывный сигнал y(t), и как дискретную последовательность y[nT].

Импульсным фильтром считают импульсный элемент (ключ) с непрерывной частью Wo(s) на выходе. За истинный сигнал фильтра принимают выходную последовательность только в дискретные моменты времени y[nT], где n = ..., -2, -1, 0, 1, 2, ...

Типовые динамические звенья

Рабочие файлы: [Звенья]

Типовые динамические звенья

Совокупность элементарных, универсальных математических функций наиболее часто используемых при построении динамических моделей реальных объектов. Представляют собой ДУ, записанные в особой форме - в виде ПФ связывающих входной и выходной сигналы звеньев. Обычно ПФ записываются не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.

Все типовые динамические звенья

1 Безинерционное звено

2 Апериодическое звено первого порядка

3 Апериодическое звено второго порядка

4 Колебательное звено

5 Консервативное звено

6 Интегрирующее звено

7 Интегрирующее звено с замедлением

8 Изодромное звено

9 Дифференцирующее звено (с минимальным замедлением)

10 Дифференцирующее звено с замедлением

Наличие нулевых корней в числителе или знаменателе ПФ типовых звеньев - это признак для разбиения последних на три группы:

Позиционные звенья: 1, 2, 3, 4, 5, - не имеют нулевых корней, и, следовательно, в области низких частот (т.е. в установившемся режиме), имеют коэффициент передачи равный k.

Интегрирующие звенья: 6, 7, 8, - имеют нулевой корень-полюс, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к бесконечности.

Дифференцирующие звенья: 9, 10 - имеют нулевой корень-ноль, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к нулю.

Точность в типовых режимах

Рабочие файлы: [ok_ast.vsm]

Для оценки точности используется величина ошибки в различных типовых режимах. Типовые режимы движения состоят в подаче на вход сигналов с нормированными метрологическими характеристиками. Различают типовые режимы:

Ненулевое, неподвижное состояние.

Движение с постоянной скоростью.

Движение с постоянным ускорением.

Движение по гармоническому закону.

Требования к ВЧ части желаемой ЛАЧХ

В качестве типовых в НЧ части используются ЛАЧХ с наклоном не более -40 дБ/дек, которому соответствует нулевой запас по фазе, поэтому необходимо в области частоты среза формировать участок с наклоном

-20 дБ/дек, т.е. сводить типовые ЛАЧХ к одному из 2-х видов:

1-2-1-2-3 0-1-2-1-2-4    ...

1-2-3 0-1-2-3-4 ...

Запретные зоны на ЛАЧХ определяют:

Для ЛАЧХ вида 2-1-2: а) начало корректирующего участка - Т2; и б) его длину - h = Т2/SТi, где i = [3, 4, ...), и w3 = w2h

или wср = w2M/(M-1)

или w3 = wср(M+1)/M.

Для ЛАЧХ вида 1-2 максимальное значение суммы постоянных времени равно SТi, где i = [1, 2, ...).

Если выше частоты среза имеется пик от колебательного звена, то его амплитуда не должна приблизиться к окружности с заданной колебательностью M, т.е. не должна достичь уровня на ЛАЧХ 20lg M/(M+1); а постоянная времени, при определении h, должна войти в сумму как 2zT.

Требуемые программные пакеты

Электронное руководство к лабораторным работам вошедшее в учебно-методический комплекс (файл tau_knv.chm) выполнено в соответствии со стандартом Windows-HTML-справки. Оно представляет собой один файл, в котором заархивированы html-страницы, учебные модели (рабочие файлы программ VisSim и Electronics Workbench), рисунки и необходимые скрипты. Файл пособия автоматически распознается и запускается операционной системой Windows 98 (NT, 2000), точнее браузером MSIE версии не ниже 4.0. Пользователям Windows 95 (NT) возможно потребуется установить Windows-HTML-справку. Для чего следует найти установочный файл hhupd.exe (733 KB).

Для организации учебного процесса следует получить пакет VisSim FAP 3.0 по "Бесплатной Академической Программе" (http://www.vissim.com). См. также сайт "VisSim в России" (http://www.vissim.nm.ru). Большинство работ можно выполнить, используя старую версию пакета - VisSim 1.2, в которой нет годографа Найквиста и оптимизации. Достоинство этого варианта в том, что руководство, модели и пакет умещаются на одной дискете и легко могут быть предоставлены студентам для самостоятельной работы дома. В первой работе имеется ссылка на демонстрационный файл csd_new.scm, который можно получить по адресу http://www.vissim.com/downloads/demos.html. В форме нужно отметить пункт «Control system design demo». Отсутствие файла может быть компенсировано рассказом преподавателя о пакете.

Требуемая версия пакета Electronics Workbench - 4.1. Часть моделей имеет настройки элементов отличные от библиотечных. Замечено, что старшие версии программы не считывают их из файлов. Адрес сайта изготовителя -

http://www.electronicsworkbench.com.

Обновленные версии руководства доступны на сайте "VisSim в России". Архив руководства можно получить по электронной почте, направив письмо-запрос автору (klinacherv_nv@mail.ru). При возможных изменениях в адресах рекомендуется воспользоваться поисковыми системами, используя ключевые слова: VisSim, симуляция движения, моделирование, Nikolay Klinachyov.

Учебно-методический комплекс

Оглавление | Введение. Классификация САР | 1. Составление исходных ДУ САР

| 2. Описание САР в частотном домене | 3.

Типовые динамические звенья | 4. Принципы и законы регулирования | 5. Устойчивость САР | 6.

Оценка качества регулирования | 7. Повышение точности САР | 8. Коррекция САР | 9. Синтез САР | 10. Системы с переменными параметрами | 11. Системы с запаздыванием | 12. Системы импульсные | 13. Системы цифровые |

Литература

Уровни сложности задач расчета цепей преобразования энергий

Тип источников движущих сил и вид требуемой в итоге расчета информации о режиме работы цепи преобразования энергии позволяют выделить пять подходов к решению, отличающихся необходимостью использования разных математических аппаратов с повышающимся уровнем сложности:

Расчет цепей с постоянными движущими силами

Расчет цепей с синусоидальными движущими силами

Расчет цепей с периодическими движущими силами

Расчет цепей с непериодическими движущими силами

Расчет цепей с волновыми процессами

Задачи принадлежащие первому уровню просты, и для их решения используются четыре математические операции: +, -, *, /. При решении задач второго уровня требуется выполнять упомянутые операции с величинами меняющимся по синусоидальному закону, поэтому используются либо "расчеты по модулям" (теорема Пифагора + векторная диаграмма), либо аппарат комплексных чисел. Третий уровень весьма условен. Здесь предполагается представление периодических движущих сил рядом Фурье и получение итогового результата согласно принципу суперпозиции с возвращением ко второму уровню, при выполнении расчетов для каждой из гармоник. Четвертый уровень предполагает описание энергетической цепи дифференциальными уравнениями и обычно используется для уточнения переходных режимов работы. На пятом уровне требуется решать дифференциальные уравнения в частных производных, учитывая индивидуальную геометрию энергетической цепи.

Условие устойчивости. Типы границы устойчивости

Устойчивость систем зависит от корней характеристического уравнения, поскольку его решение есть сумма экспоненциальных функций:

.

Рассмотрим варианты свободного движения систем от ненулевого начального положения:

Заметим, что:

C1 e -(a+jb)t

+ C2 e -(a-jb)t

= A e -at sin(bt+j) ,

где: A и j - новые постоянные интегрирования, a - показатель затухания,

b - круговая частота затухающих колебаний.

Таким образом, для затухания переходного процесса и устойчивости линейной системы необходимо и достаточно, чтобы вещественные части корней были отрицательными, те лежали слева от мнимой оси плоскости корней.

Система будет находиться на границе устойчивости при наличии:

нулевого корня,

пары чисто мнимых корней,

бесконечного корня.

Устойчивость и качество регулирования систем с var-параметрами

Поскольку в квазистационарных САР параметры меняются много медленней свободного движения системы, параметрическую САР считают устойчивой, если при всех "замороженных" комбинациях параметров она остается устойчивой.

Т.е. в параметрической ПФ W(s,t) фиксируют время t в диапазоне 0 < t < T

и многократно исследуют на устойчивость, используя любой из критериев. Максимальное внимание надо уделить временным интервалам, где параметры меняются быстро или происходит смена знака. Особенно эффективно использование корневого годографа, зависимого от var-параметра, для оценки тенденций в системе.

При оценке качества регулирования следует учитывать, что коэффициенты ошибок получаются зависимыми от времени: Ck = [dkFx(s, t) / dsk], при s=0.

Изменение параметров можно рассматривать как возмущающее воздействие на систему. Соответственно составляющие ошибки от var-параметра не будут сводиться к нулю, за исключением случая, когда содержащее var-параметр звено установлено в цепи ОС или в прямом канале до интегрирующих элементов. Поскольку динамика изменения var-параметров в сравнении с динамикой задающего воздействия g(t) не значительна в случае квазистационарных систем, то соответствующие составляющие ошибок: по скорости, ускорению, ... - как правило, меньше.

Устойчивость САР

Рабочие файлы: [Начальные условия / Параметры & Устойчивость]

Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Понятие устойчивости можно распространить и на случай движения САР:

невозмущенное движение,

возмущенное движение.

Устойчивость систем с запаздыванием

Рассмотрим замкнутую систему:

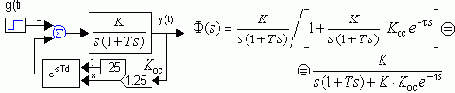
По знаменателю ПФ F(jw) видно, что в общем случае характеристическое уравнение будет иметь множитель e-ts, который определяет возможность наличия бесконечного количества корней (см. петли годографа Михайлова D(jw)).

Как и прежде, для устойчивости все они должны иметь отрицательные вещественные части.

Для устойчивости систем 1-ого и 2-ого порядка с запаздыванием не достаточно положительности коэффициентов.

Для систем 3-его и более порядков не применимы критерии Вышнеградского, Рауса, Гурвица.

V - Преобразование. Билинейные преобразования. Устойчивость и качество импульсных систем

Рабочие файлы: [Аппроксиматоры] [bi_line_sz.vsm]

Построим область устойчивости в плоскости комплексной величины z. Воспользуемся методикой D-разбиения и, меняя частоту w

от - Ґ до + Ґ, получим границу z = eTs = e jwT - в виде окружности единичного радиуса, внутрь которой попадает левая полуплоскость комплексной величины s. Следовательно, для устойчивости, все корни-полюсы замкнутой системы F(z)

должны находится внутри этой окружности.

Итак, для описанных с помощью аппарата Z-преобразования импульсных систем, всилу изменившегося вида области устойчивости и периодичности их ЧХ W(e jwT), разработанные для непрерывных систем критери устойчивости (кроме критерия Найквиста и корневого годографа), а так же наиболее эффективные методы коррекции и синтеза (использующие ЛАЧХ & ЛФЧХ) не приемлемы.

Для преодоления этого затруднения используют v-преобразование, которое отражает окружность единичного радиуса на мнимую ось комплексной величины v, с помощью подстановки:

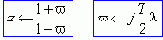
Физически подстановка означает переход к ДУ заменой в РУ элементов чистого запаздывания грубой аппроксимацией - одним фазосдвигающим звеном.

Вторая формула для перехода в область псевдочастот l

получена из соотношения:

,

отметим так же, что:

.

v-Домен и домен псевдочастоты

l используют редко, поскольку для большинства импульсных и цифровых систем частота дискретизации 1/T выбирается в 6...10 раз больше частоты среза. В таком случае выполняется условие wсрT<2, вследствие чего в полосе системы псевдочастота l и частота w практически совпадают. Поэтому обходятся доменом обычных частот, а для переходов используют формулы "Билинейного преобразования":

Резюме:

После v-преобразования, используя ПФ W(v) или F(v) можно применять обычные (в основном алгебраические) критерии устойчивости, справедливые для непрерывных систем.

После последующего перехода в область псевдочастот (подстановка

v = jlT/2) вид ПФ W(jlT/2)

и F(jlT/2)

становится пригоден для применения медодов, использующих ЛАЧХ & ЛФЧХ.

Качество импульсной системы может оцениваться построением кривой переходного процесса, что при использовании ПФ F(z) сравнительно легко.

Оценку качества в установившихся режимах удобно выполнять нахождением коэффициентов для разложения ошибки в ряд:

,

которые являются коэффициентами разложения ПФ Fx(z) в ряд Маклорена по степеням s:

,

где: z = e Ts.

Вопросы к экзамену по курсу ТАУ

Примеры автоматических систем. Принципы автоматического регулирования. Классификация автоматических систем. Программы и законы регулирования. Демонстрационные примеры адаптивных систем.

Линеаризация дифференциальных уравнений (ДУ) систем автоматического регулирования (САР). Геометрическая трактовка линеаризации. Формы записи линеаризованных уравнений. Единичная функция, дельта-функция, переходная функция и функция веса. Частотная передаточная функция (ПФ), частотные характеристики. Позиционные звенья. Интегрирующие звенья. Дифференцирующие звенья. Составление исходных ДУ САР (форма Коши; решенные относительно: ошибки, относительно регулируемой величины). ПФ используемые для описания систем (W(p), Wf(p), Ф(p), Фх(p)). Линейные непрерывные законы регулирования (пропорциональное регулирование, интегральное регулирование, изодромное регулирование, регулирование с использованием производных).

Понятие устойчивости для линейных САР. Условия устойчивости, типы границы устойчивости. Необходимое условие устойчивости САР, достаточное для систем 1-ого и 2-ого порядков. Критерий устойчивости Гурвица. Критерий устойчивости Михайлова. Свойства, примеры годографов Михайлова. Построение областей устойчивости D-разбиение. Критерий устойчивости Найквиста. Свойства, примеры годографов Найквиста. Определение устойчивости по ЛАЧХ & ЛФЧХ. Методика построения асимптотических ЛАЧХ & ЛФЧХ линейных систем.

Основные подходы к оценке качества систем и общие понятия о соответствующих критериях. Точность САР в типовых режимах. Коэффициенты ошибок. Оценка запаса устойчивости и быстродействия по переходной характеристике. Корневые методы оценки качества (колебательность, степень быстродействия). Понятие о среднегеометрическом корне. Мажоранта и миноранта переходного процесса. Интегральные оценки качества (линейная, квадратичная, улучшенная). Частотные критерии качества. Показатель колебательности.

Постановка задачи повышения точности систем, обзор используемых методов. Увеличение коэффициента усиления разомкнутой цепи, как метод повышения точности.
Повышение степени астатизма, как метод повышения точности. Применение регулирования по производным, как метод повышения точности. Комбинированное управление. Введение неединичных обратных связей.
Постановка задачи коррекции систем, обзор используемых методов. Способы введения корректирующих звеньев. Практическая реализация последовательных корректирующих звеньев. Демпфирование с подавлением высоких частот. Демпфирование с подавлением средних частот. Демпфирование с подавлением низких частот или эквивалентным поднятием высоких. Демпфирование с введением отрицательных фазовых сдвигов. Применение корректирующих обратных связей.
Постановка задачи синтеза систем, обзор используемых методов. Метод логарифмических амплитудных характеристик. Требования к низкочастотной части (НЧ) желаемой ЛАЧХ. Построение НЧ части желаемой ЛАЧХ. Требования к высокочастотной части (ВЧ) желаемой ЛАЧХ. Построение ВЧ части желаемой ЛАЧХ. Корневой метод синтеза. Метод корневых годографов.
Системы с переменными (var) параметрами и их реакции на стандартные возмущения 1(t) и d(t). Отыскание ПФ систем с var-параметрами. Устойчивость и качество регулирования систем с var-параметрами. Синтез параметрических систем.
Системы с запаздыванием; ПФ звена чистого запаздывания. Линеаризованные аппроксиматоры звена времянного запаздывания, вопросы адекватности. Устойчивость и качество регулирования систем с запаздыванием.
Импульсные системы; виды модуляции. Типовая структура импульсной системы. Решетчатые функции. Математические операции с решетчатыми функциями. Разностные уравнения. Z-преобразование. Математическая модель реального импульсного элемента. Понятие дискретной ПФ. Правила преобразования структурных схем дискретных систем. ПФ системы с экстраполятором нулевого порядка и звеном запаздывания. ПФ системы с экстраполятором, осуществляющим АМ первого и второго рода. ПФ замкнутой дискретной системы (для регулируемой координаты, для ошибки, для возмущений). Дискретная синусоидальная последовательность, теорема Котельникова, частота Найквиста.Частотные ПФ импульсных систем. Устойчивость и качество импульсных систем. W-преобразование.
Системы с ЦВМ, общие понятия. Процессы, протекающие в системах с ЦВМ. Методика вывода дискретных ПФ. О синтезе систем с ЦВМ методом логарифмических амплитудных характеристик. Дискретная коррекция. Дискретное представление непрерывных регуляторов. Модифицированные законы регулирования. Алгоритмы составления программ, реализующих ПФ на ЦВМ. Примеры составления программ для ЦВМ.

Мир технических систем разнообразен. Однако

Мир технических систем разнообразен. Однако математика и физика выявили простые параллели в этом сложном мире. Можно выделить ряд энергетических доменов, которым принадлежат те или другие системы или их модули. Это электрический, магнитный, термальный, гидравлический, акустический, механический и ротационный домены. Так же существуют два фундаментальных постулата. Первый постулат гласит, что материя не может появиться ни откуда и не может исчезнуть в никуда. Второй постулат утверждает то же самое в отношении энергетического потенциала. Эти постулаты имеют частные формулировки для каждого энергетического домена. Например, для электрического домена это первый и второй законы Кирхгофа. Каждый из энергетических доменов характеризуется двумя физическими величинами первого и второго рода. В случае электрического домена - это электрические ток и напряжение соответственно. Эти парные физические величины, в каждом энергетическом домене, связаны между собой законом Ома в соответствующей формулировке (существуют: электрическое, магнитное, термальное, гидравлическое, акустическое, механическое и ротационное сопротивления). Так же следует отметить, что произведение физических величин первого и второго рода всегда есть мощность.
Представленная система параллелей позволяет понять, что математическое описание процессов движения координат систем принадлежащих разным энергетическим доменам подобно, и может быть предметом изучения одной науки, которая называется "Теория систем автоматического регулирования". Более того, в последние годы, приобретен успешный опыт применения методов этой теории при решении задач управления в экономических, финансовых и других нетехнических системах.


Известно много хороших математических программ. Отнесем каждую к одной из двух групп:
Мощные калькуляторы для статических вычислений (Matcad, Mathematica, Maple).
Специализированные решатели для моделирования динамических процессов (DyMoLa, Dynast, Multisim, VisSim, MBTY, MVS, Simulink).
При использовании программ и той, и другой группы пользователю нужно определить последовательность математических функций, которые должны быть вычислены математическими ядрами. Фундаментальное отличие проявляется в том, что при использовании программ-калькуляторов пользователь должен рассчитывать лишь на однократное вычисление запрограммированной им последовательности функций, а при использовании динамических решателей может использовать возможности повторных вычислений. Таким образом, с одной стороны, если в вашем распоряжении программа-калькулятор, то вам нужно знать громадное количество методов, позволяющих сократить количество математических операций [2] (что спасет вас от мозоля на пальце). А с другой стороны, нельзя поспорить с тем, что при использовании динамических решателей для решений задач "в лоб" (т.е. в четком соответствии с их физической природой, без использования накрученных на физическую природу математических абстракций второго, третьего порядка или жестко формализованных (матричных) подходов), придется серьезно загрузить "бедный" процессор компьютера несколькими миллиардами математических операций аж на две или даже десять секунд.
Но оставим иронию. Компьютеры, безусловно, изобретались не для офисных приложений. Мозг же студента развивается не существенно от запоминания большого количества формализованных или жёстко алгоритмизированных методик, которые разрабатывались еще до появления компьютеров в целях уменьшения количества вычислений. Эти факты объясняют существенный интерес ведущих педагогов к программам математического моделирования динамических систем. Однако ограничения в доступности подобных программ, стремление производителей скрыть технологии их функционирования, плюс всенародная любовь к "калькуляторам" сдерживают их широкое распространение, порождают недоверие к ним, что, в конечном счете, сказывается на их качестве.
Статья раскрывает идеи и решения, составляющие основу программ математического моделирования динамических систем. Автор высказывает надежду, что статья разрушит хотя бы часть "барьеров недоверия" и будет способствовать появлению новых поклонников у "динамических решателей". Возможно, часть описанных решений будет использована разработчиками моделирующих программ, студентами-дипломниками и аспирантами.
Хотелось бы сказать несколько благодарственных слов корпорации Microsoft, которая, продавая свои готовые приложения за деньги, достаточно часто распространяет технологии, с помощью которых они были созданы на бесплатной основе.

Введение в дисциплину "Основы моделирования систем"

Рабочие файлы: []

Моделирование

1)Искусство построения истинных или ложных (по соответствию физической природе) моделей систем.

2) Совокупность действий по созданию модели реальной системы, последующая цель которых – изучение природы системы, возможностей ее структурного развития или прогнозирование поведения.

Симуляция движения

Процесс движения координат модели направленный на получение адекватных результатов.

Модели систем могут иметь разную физическую природу. Компьютеры и соответствующее ПО являются наиболее адаптивными физическими объектами, из тех, которые могут быть основой для построения моделей. Дальнейшее изложение связано с программами математического моделирования динамических систем, к которым относятся: VisSim, Simulink (MATLAB), SystemBuild (MATRIXx), Anylogic (Model Vision Studium), MBTY, 20-sim, ITI-SIM, DyMoLa, SIMPLORER, DYNAST, hAMSter, Easy5, DASE и др.

Введение в технологию моделирования на основе направленных графов

Графов теория

Учение об общих топологических свойствах графов и о вытекающих из них расчетных методах. Две ветви теории: теория направленных графов и теория ненаправленных графов являются основой для технологий структурного

и мультидоменного физического моделирования.

Граф направленный (сигнальный)

Диаграмма прохождения сигнала, состоящая из совокупности узлов (сумматоров) и соединяющих их ветвей. Стрелки на ветвях указывают направление передачи сигнала или воздействия от одного узла к другому. Ветви в направленном графе характеризуются передаточными функциями. Направленный граф является графической формой записи системы уравнений описывающих динамическую систему, и не может отражать ее топологию (модульную структуру).

Узел направленного графа

Сумматор координат модели динамической системы с одним выходом (поэтому узел направленного графа называют координатой). Обычно в каждом энергетическом домене в качестве координат выступают парные физические величины, чье произведение есть мощность. В пакетах математического моделирования эти парные физические величины называются координатами первого и второго рода. Выходные координаты ветвей собираются в узлы направленного графа согласно постулатам о сохранении материи и энергетического потенциала (первый и второй законы Кирхгофа1). Узлы направленного графа, ровно как и сам граф, не отражают различий в физической природе координат первого и второго рода (это непреодолимый недостаток направленных графов).

Ветвь направленного графа

Графический образ закона преобразования сигнала, который называется передаточной функцией. Если направленный граф есть истинная модель

динамической системы и узлы графа отражают все ее координаты (граф не приведен), то передаточные функции ветвей есть либо закон Ома2, сформулированный для соответствующего энергетического домена и связывающий его

физические величины первого и второго рода, либо другие физические законы, связывающие физические величины первого и второго рода разных энергетических доменов.

Контур
Для направленных и ненаправленных графов, это замкнутый путь, проходящий через несколько узлов и ветвей.
1)Для каждого энергетического домена разработаны альтернативные, матричные методы расчета соответствующих систем. Например, в электрическом домене к ним относятся: "Метод контурных токов", "Метод узловых потенциалов" - они тоже могут использоваться для составления графов. Вспомним цель разработки этих методов. Она состояла только в одном - в сокращении размерности системы уравнений, причем за счет отдаления математического описания от физического смысла. Компьютерное моделирование понижает ценность этих методов, поэтому для унификации подхода рекомендуется составлять графы согласно методу расчета, использующему первый и второй законы Кирхгофа.
2) И для одного энергетического домена закон Ома может иметь несколько форм записи. Например, для электрического домена формула закона Ома отлична для активного сопротивления, индуктивного и емкостного.

Введение в технологию мультидоменного физического моделирования с применением ненаправленных графов

Главной задачей, решаемой программами математического моделирования динамических систем, является симуляция движения их координат. Сегодня можно выделить два эволюционных этапа развития решателей этих программ. На первом этапе в программах появляется явный решатель. Это библиотека классических подпрограмм (функций), которые реализуют операцию интегрирования. Таким образом, используя дискретные квази-аналоги интеграторов, пользователь может решать дифференциальные уравнения. Лишь на втором этапе в моделирующих программах появляется неявный решатель. Это библиотека классических подпрограмм, которые предназначены для итерационного поиска корней алгебраических уравнений.

Если моделирующая программа может грамотно использовать неявный решатель, то из программы для моделирования систем автоматического регулирования она может перейти в разряд программ для мультидоменного моделирования физических систем, с применением схем физических принципиальных (например, электрических).

Основу представляемой технологии моделирования составляют модели девяти примитивов, которые используются при составлении схем замещений. Упомянутым примитивам (моделям) присвоены условные графические обозначения, заимствованные из схем электрических принципиальных, но суть моделей распространяется на любой из семи энергетических доменов: электрический, магнитный, тепловой, гидравлический, акустический, механический и ротационный.

Выбор шага симуляции и метода интегрирования

Рабочие файлы: [Шум сопроцессора]

Шаг симуляции

Фундаментальный параметр процесса симуляции компьютерной модели. Равен интервалу между временными значениями, для которых вычисляются все координаты модели (т.е. рассчитывается весь поток процедур и функций реализующий модель).

При компьютерном моделировании существенными следует считать четыре источника погрешности:

Трансцендентные функции, которые вычисляются компьютером путем аппроксимации полиномиальными или степенными рядами:

Дискретный квазианалог интегратора (блок 1/S).

Итерационный решатель (тот или иной классический алгоритм, предназначенный для решения алгебраических уравнений путем подбора независимых переменных до заданной точности).

Математический сопроцессор компьютера, чья дискретная природа требует округлений, которые, в свою очередь, обычно проявляются в виде шума при дифференцировании меняющихся в большом диапазоне параболических сигналов n-ого порядка.

Погрешности дискретных квазианалогов интеграторов играют решающую роль в компьютерном моделировании. На рисунке показано, как дискретный квазианалог интегратора (блок 1/S) обрабатывает сигнал синусоидальной формы. Наглядно видно, что при уменьшении шага симуляции погрешность интегрирования дискретным квазианалогом интегратора снижается. Это основное правило, которому надо следовать при настройке параметров симуляции.

Очевидно, что разные методы дискретного интегрирования будут иметь разные величины погрешности. Эту погрешность лучше представить в виде декомпозиции на амплитудную и фазовую составляющие и оценивать их величины в частотном домене. Максимальное влияние проявляется от фазовой погрешности.

Простейшая модель синусоидального генератора на двух интеграторах позволяет убедиться в том, что погрешности всех классических методов интегрирования лежат в том диапазоне, который определен двумя методами Эйлера с запаздыванием и с упреждением. Таким образом при выборе шага симуляции следует уменьшать его до тех пор, пока вариация переходного процесса (от переключения упомянутых методов) не будет укладываться в заданный допуск.

Переходные процессы в системе вызваны ненулевыми начальными условиями. Частотная характеристика разомкнутой системы очевидна (-40дБ/дек. & -180°). Методу Эйлера с запаздыванием соответствует расходящийся переходный процесс; методу Эйлера с упреждением – сходящийся; методу трапеций – синусоида с постоянной амплитудой

Вычисление коэффициентов цифровых фильтров

Аналоговые прототипы разрабатываются для приведенной (нормализованной) частоты. Данные прототипы, при оптимальной настройке, являются фильтрами Баттерворта (с максимально плоскими ЛАЧХ). Билинейное преобразование выполняется посредствам подстановки:

1 1 - z^-1 s = -------------- * ---------- tan(omega/2) 1 + z^-1

Для вычисления тангенса при составлении программы используются тригонометрические тождества:

sin(w) 1 - cos(w) tan(w/2) = ------------ (tan(w/2))^2 = ------------ 1 + cos(w) 1 + cos(w)

Вычислительные алгоритмы идентификации частотных характеристик моделей

Рабочие файлы: [fr_ABCD.mcd] [fr_ABCD_sz.mcd]

Главная особенность вычислительных алгоритмов идентификации ЧХ состоит в том, что они ни коим образом не анализируют входной и выходной сигналы, а поэтому могут применяться только к математическим моделям. Исходной информацией для расчета ЧХ являются коэффициенты модели, поэтому предварительная процедура её идентификации является обязательной.

Если программе известны коэффициенты числителя и знаменателя ПФ модели, то алгоритмизация процедуры расчета ЧХ не вызывает затруднений. Гораздо чаще программы математического моделирования располагают результатом идентификации в матричной ABCD-форме. Выведем формулу расчета ЧХ для данного случая:

ЧХ дискретной системы так же можно рассчитать с помощью представленной формулы, но нужно выполнить постановку: jw¬ е jwT. В случае если требуется построить частотную характеристику для домена псевдочастоты l (что может потребоваться при использовании устаревших методик), требуемая подстановка имеет вид: jw ¬ (2+

jlT)/(2- jlT).

Если же система является мультичастотной дискретной, гибридной, или же непрерывной, но со звеньями чистого запаздывания, то требуется корректное заполнение диагональной матрицы соответствующими частотными операторами. На сегодняшний день достоверность результатов в этом случае требует подтверждения методами основанными, на анализе входных и выходных сигналов.

Во избежание необоснованных обвинений моделирующих программ, каждый специалист должен знать, что рассчитанная на основе известных коэффициентов ЧХ ни как не учитывает тех погрешностей, которые не может не вносить ЦВМ, согласно своей природе, в процесс симуляции моделей (см. рис.). Например, для перехода в частотную область используется подстановка идеального частотного оператора s ¬ jw

(без вещественной составляющей), который не учитывает погрешностей дискретных квазианалогов интеграторов моделирующих программ (что, впрочем, методически верно).

На рисунке показаны переходные процессы системы, вызванные ненулевыми начальными условиями. Частотная характеристика разомкнутой системы очевидна (-40 дБ/дек. & -180°), и вычислительные алгоритмы

частотного анализа ее подтверждают. Но симуляция движения координат модели выявляет несоответствия между временным и частотным доменами при переключении методов интегрирования (методу Эйлера с запаздыванием соответствует расходящийся переходный процесс; методу Эйлера с упреждением – сходящийся; методу трапеций – синусоида с постоянной амплитудой)

Для максимально плавного преодоления кризиса

Для максимально плавного преодоления кризиса в методике преподавания дисциплин связанных с расчетом цепей преобразования энергий требуется выполнение следующих условий.
Преподаватели не должны скрывать, от студентов тот факт, что большинство изучаемых методик расчета цепей доживают последние дни, поскольку были рассчитаны на ручные вычисления.
Надо признать, что использование в учебном процессе для расчета цепей преобразования энергий широко известных математических программ для статических вычислений (Matcad, Mathematica, Maple) не даст положительного методического результата.
Вузы России должны покупать специализированные программы для моделирования динамических процессов. Покупки должны быть централизованы. Программу должен покупать вуз, а не кафедра. Только в этом случае вузы смогут заставить разработчиков раскрыть технологии функционирования программ. Кроме того, вуз – это не рядовой потребитель (юзер), поэтому покупку каждой новой версии вуз должен превращать в финансирование нужных ему доработок в программе.
Вузам требуется существенно увеличить количество аудиторий оборудованных компьютерной проекционной аппаратурой. Мел доска и текст, как средства обучения, должны уйти в прошлое.
Каков же прогноз протекания кризиса, если мы как всегда, дружно и все вместе, вспомним о нашей любимой поговорке: "Работа – не волк – в лес не убежит"? На взгляд автора через пятнадцать лет студенты будут заваливать преподавателей задачами прорешанными, к тому времени в чуть более совершенных программах. И преподавание фундаментальных технических дисциплин превратиться в такую же профанацию, какую мы имеем сегодня в тех гуманитарных дисциплинах, технология освоения которых предполагает написание реферативных работ.
Чем же страшен этот кризис? Ведь он, как и многие другие, будет пережит нами. Главная опасность в том, что существует не один, а два сценария посткризисного развития. Согласно первому сценарию в России появится еще ряд профессий, для которых будет справедливо высказывание Бернарда Шоу: "Всякая профессия – есть заговор против непосвященного". И последующие 50 лет мы будем говорить о необходимости "прозрачности" не только в финансовой отчетности предприятий, но и в технических решениях. (Кто сегодня помнит о том, что еще не так давно нельзя было продать телевизор или магнитофон без схемы электрической принципиальной)? Согласно второму сценарию дисциплины связанные с теорией расчета цепей преобразования энергий действительно станут простыми и легкими в изучении. Выбирать – нам.
9.09.2003

XML хранилище модели

Анализ графических примитивов и правил, используемых для выполнения рисунков блок-схем, позволяет выявить ряд объектов и принадлежащих им атрибутов, которые требуется сохранять в файле модели. Отношения между объектами демонстрирует показанная на рис. 4 схема данных. Очевидно, что для поддержания подобной информационной структуры требуется реляционная СУБД с мощными механизмами масштабирования, поиска, сортировки, обеспечения целостности данных и сохранения.

Рис. 4. Схема данных хранилища модели

К большому сожалению разработчики моделирующих программ предпочитают реализовывать собственные СУБД. Судя по функционированию программ, для большинства эта задача оказывается сложной. Вторым досадным моментом является несовместимость хранилищ (рабочих файлов) разных производителей и невозможность их непосредственного восприятия человеком. Как было упомянуто ранее, проблему может снять бесплатный движок реляционной базы данных фирмы Microsoft — COM-сервер msxml*.dll [7], последние версии которого включены в платформу .NET.

Если ориентироваться на Visio, то данный пакет уже использует этот движок для сохранения рисунков. Однако схема данных хранилища объектов Visio отличается от представленной на рис. 4. Это означает, что она не будет оптимальной (речь о нормализации базы данных) для хранения моделей и, в частности, блок-схем. Следует так же отметить, что схема данных для хранения объектов направленного графа (блок-схемы) не подойдет для хранения объектов ненаправленного графа (схемы физической принципиальной). Но различия не существенны, поэтому последнюю не рассматриваем. Более того, при использовании хранилищ с XML-разметкой, производители моделирующих программ могут придерживаться собственных схем данных — это не ограничит пользователя. Таже СУБД предоставляет механизмы XSLT-трансформаций, позволяющие без привлечения производителей переформатировать рабочие файлы одной моделирующей программы (их структуру и синтаксис) в рабочие файлы другой программы.

Одна из возможных XML-схем хранилища направленного графа (блок-схемы) представлена в виде листинга 4 (атрибуты не показаны). Большинство реляционных отношений схемы данных (рис. 4) кодируется инкапсуляцией описания соответствующих объектов внутри тегов объектов-владельцев. Лишь отношение между таблицей входов и таблицей связей задается парными атрибутами тегов <input/> и <wire/>. При отрисовке блок-схем широко используется механизм иерархической инкапсуляции повторяющегося фрагмента модели в одном составном блоке. В хранилище такие блоки имеют тег <space/>. Принцип описания инкапсуляции можно отследить по положению тегов <block/>.

Листинг 4

<!-- XML-схема хранилища направленного графа (рисунка блок-схемы) -->

<!-- Created by ModelStoreGate.WSC.1.00 -->

<directed_bond_graph> <block> <space> <block>...</block> <block>...</block> ...

<input /> ... <output> <wire /> ... </output> ... </space> <param /> ... <input /> ... <output> <wire /> ... </output> ... <model> <name /> <simproperties /> <autor /> <data /> <description /> <ico /> <library /> </model> </block> </directed_bond_graph>

Для создания хранилища и записи его на диск под управлением СУБД msxml*.dll требуется промежуточный COM-сервер, который допустимо написать на скриптах VBScript или JScript [6], но лучше на VB. Листинг 5 демонстрирует порядок использования объекта ModelStoreGate.WSC из этого сервера для экспорта блок-схемы. Сравнение листингов 2 и 5 позволяет выявить их подобие, из которого следует возможность использования шлюза Visio2SimKernel не только для программирования математического ядра, но и для экспорта рисунка блок-схемы в рабочий файл модели той или иной моделирующей программы.

Листинг 5

/* ************************* Head ***************************** */

// Определяем имя рабочего файла блок-схемы



NameMakingFile = "MDL_01c.XML";

// Создаём из COM-сервера объект для работы с хранилищем

var Store = new ActiveXObject("ModelStoreGate.WSC"); Store.reConnectToLibrary("1stSim_Lib_V2b.xml"); Store.ModelName = "K/(1+Ts) on SUB_1/S"; Store.ModelTimeStart = 0; Store.ModelTimeStep = 0.01; Store.ModelTimeEnd = 1; Store.ModelSimMode = 0; Store.Autor = "Nikolay Klinachyov"; Store.Date = "10.11.2003"; Store.Description = "Модель апериодического звена " + "на субмодели дискретного квазианалога интегратора"; Store.Ico = "apper.ico";

// Создаем корневой составной блок

// Определяем указатель на субобласть составного блока

rtB = Store.addBlock("L001", null);

/* ************************* Begin **************************** */

// Создаем блоки внутри корневого составного блока

Store.addBlock("L701", rtB); // 1(t-dT)

Store.addBlock("L101", rtB); // summingJunction

Store.addBlock("L100", rtB); // gain

Store.addModel("SUB_1S.XML", rtB); // 1/S: 6+1 блок

Store.addBlock("L800", rtB); // export

// Добавляем дополнительные входы и выходы блокам

// Store.addInput(2);

// Store.addOutput(0);

// Устанавливаем параметры блоков и начальные условия

Store.setParam( 1, 1, 1.0); Store.setParam( 1, 2, 0.05); Store.setParam( 2, 2, -1.0); Store.setParam( 3, 1, 4.0);

// Создаем связи между блоками (схему передачи аргументов)

Store.addWire( 1, 1, 1, 2); Store.addWire( 2, 1, 1, 3); Store.addWire( 3, 1, 1, 4); Store.addWire( 4, 1, 2, 2); Store.addWire( 2, 1, 1,11); Store.addWire( 4, 1, 2,11);

/* ************************* End ****************************** */

// Сохраняем хранилище в файле

Store.save( NameMakingFile ); // WScript.Echo("File " + NameMakingFile + " successfully created");

// Store.visualizationInMSIE( NameMakingFile );

Фактически, объект ModelStoreGate.WSC отвечает за трансформацию линейного потока команд в иерархическое хранилище.Безусловно, при считывании рабочего файла в целях визуализации редактором векторной графики или же для прямого программирования математического ядра требуется обратное преобразование. Оно может быть выполнено одной процедурой с соответствующими параметрами, примером которой является командный скрипт XML2SimKernelGate.WSF см. рис. 2.

Z-преобразование

Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа:

которое называется Z-преобразованием при подстановке z = eTs, и связывает изображение с оригиналом.

Z-преобразования (изображения) типовых решетчатых функций и типовых непрерывных ПФ W(s) сведены в таблицы. Определены правила и теоремы для математических манипуляций с ними.

Запись линеаризованных уравнений в стандартных для ТАУ формах

Представим линеаризованное уравнение (*) в форме уравнения движения и в виде ПФ.

Уравнение движения предполагает: а) выходную величину и ее производные в левой части уравнения, а входную и все остальные члены - в правой; б) так же, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести линеаризованное уравнение (*) к такому виду введем обозначения:

тогда:

T33Dy''' + T22Dy'' + T1Dy' + Dy = k1Dx1

+ k2Dx2 + k3Dx'2

+ k4 f1 .

Знак D обычно опускают и записывают уравнение в символьном виде:

(**)

(T33 p3 + T22 p2

+ T1 p + 1) y

= k1x1 + (k2

+ k3 p) x2

+ k4 f1 ,

где:  

 

T3, T2, T1

- постоянные времени;

k4, k3, k2, k1

- коэффициенты усиления;

p=d.../dt - оператор дифференцирования.

Для вывода ПФ решим уравнение движения (**) относительно выходной величины:

y = W1(p) Dx1

+ W2(p) x2 + Wf (p)  f1 ,

Более строго передаточные функции определяются через изображения Лапласа или Карсона-Хевисайда, как отношение изображений выходной и входной величин:

.

Запись ПФ для переменных во времени величин и для их изображений совпадает до оператора. В первом случае ПФ зависит от оператора дифференцирования p=d.../dt. Во втором случае - от оператора Лапласа s=c+jw.

Заземлитель потенциала

Модель заземлителя потенциала состоит из одного блока constraint. Данный датчик неявного решателя будет уравновешиваться теми блоками unknown

(с красной рамкой), что будут обнаружены в источниках той энергетической цепи, которую составит пользователь моделирующей программы. При этом заземлитель может быть подключен к любому ее потенциальному контакту.

Не следует путать заземлитель энергетического потенциала с условным графическим обозначением заземления на схемах электрических принципиальных. Заземлитель потенциала – это не проводник. Он может быть установлен в модели только один раз. В программах с развитым графическим интерфейсом за подключение этого блока отвечает сама моделирующая программа.

---